Neural Networks-Perceptron

1. Introduction

 

- History of Neural Networks

 

- Neural Networks (NN)

 

A mathematical model that mimics human brain

• Data is coming - 데이터가 들어오고

• Data is connected as networks with weights - 데이터가 가중치와 함께 네트워크로 연결됨

• If function value is sufficiently strong, the node is activated - 함수값이 충분하면(threshold 이상이면) 노드가 활성화됨

 

Artificial Neural Networks (ANN)

- Most algorithm can be described as a special form of neural networks, Deep learning is a subset of NN

: 대부분의 알고리즘은 특정 형태의 NN이며 딥러닝은 NN의 한 종류이다

 

 

2. Linear Separability - 선형분리 가능성

- Linear Machine

: A linear function that separates an original space into two subspaces

: 직선 하나로 공간을 2분할 해서 분류 문제를 처리함

 

 

 

- Generalize to multivariate problem

 

 

3. Perceptron

: Frank Rosenblatt 가 1957년에 제안한 초기 형태의 인공 신경망으로 다수의 입력으로부터 하나의 결과를 내보내는 알고리즘

Input과 weight를 곱한것들을 다 더 한 summation 값을

activation function에 넣어서 나온 output 값이

임계값(θ) 이상이면 1, 작으면 0으로 출력함

 

 

- Activation Function (활성함수)

: 큰값이 들어오면 큰값이 나오고, 작은 값이 들어오면 작은 값을 출력

 

 

(1) step function

   : summation 값이 0보다 크면 1, 작으면 0

   : 끊어져있어서 미분이 불가능하다

 

 

 

 

 

 

 

 

 

(2) Logistic sigmoid (s자 곡선 함수)

   : output range가 0에서 1

   : 확률형태로 표현하기 좋음

   : 항상 양수만 나옴

   : 딥러닝 시대 이전의 default

 

 

 

 

 

 

 

 

 

(3) hyperbolic tangent

: 1과 -1 사이

: 단) 확률값이 아님

: 장) 0 센터(output의 중심을 0으로)

: LSTM, RNN, Trms 시 사용

 

 

 

 

 

4. Mutilayer Perceptron (MLP)

- Nonlinear Classification

: 퍼셉트론으로는 선형 문제가 아닌것(어려운 문제)는 풀 수 없다

  --> Mutilayer Perceptron (MLP) 제안 (Minsky)

 

[Example]

 

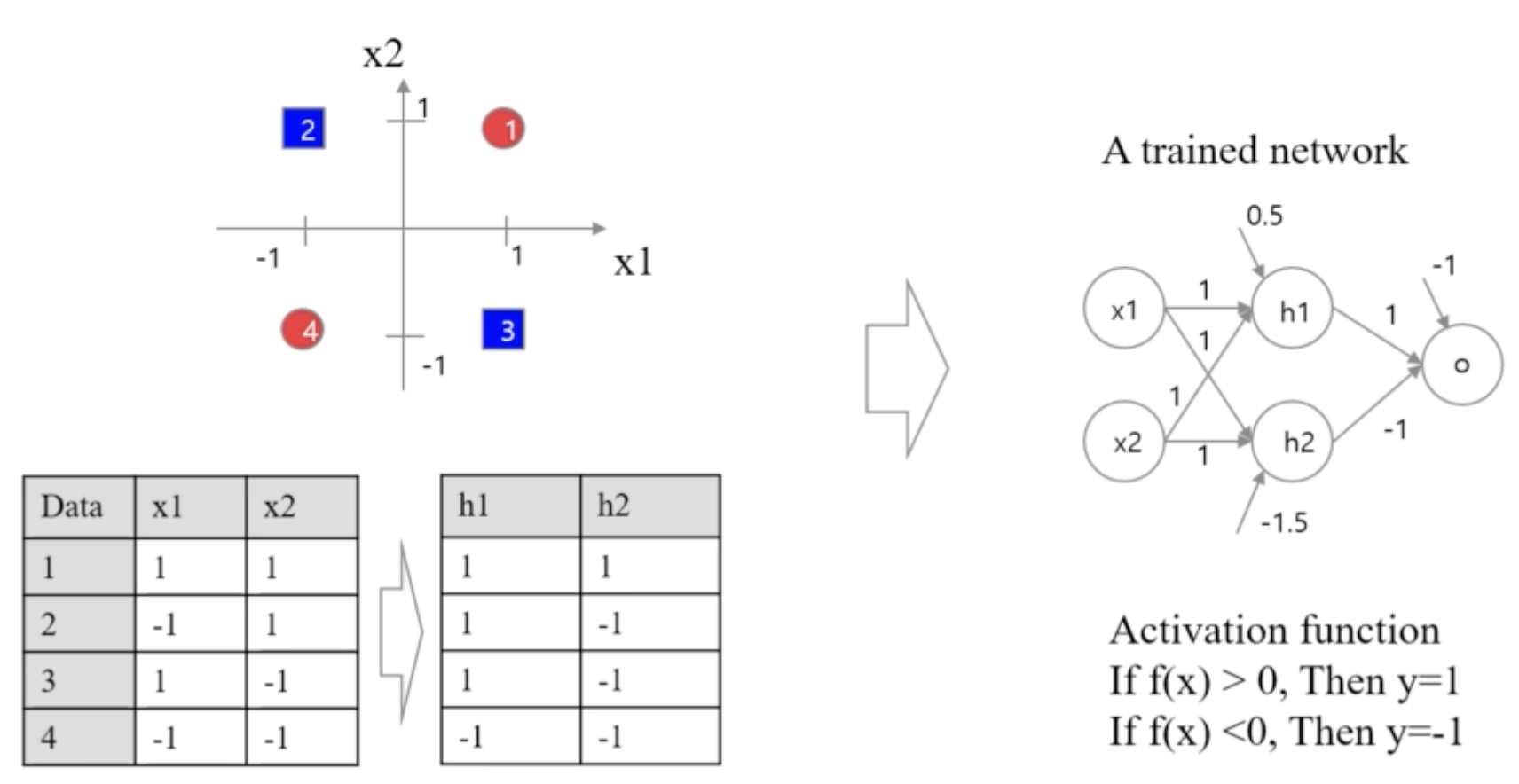
첫번째와 두번째 퍼셉트론 먼저 수행

첫번째와 두번째 퍼셉트론에서 나온 결과를 바탕으로 3층에서 다시 퍼셉트론 수행

 

- Perceptron을 다층으로 배치하여 적층구조 형성

• 1-2층에서는안풀리던문제가2-3층에서는풀림

• 적층구조로 문제 해결이 가능해졌지만, 20년동안 dark era(약 20년동안)가 있었던 이유

: 가중치를 최적화 하는 방법을 알지 못함

 

- Universal Approximation Theory

: 공간을 4번 왜곡시켜서 엠보싱을 만듦

: 3-MLP로 그 어떤 모양의 함수도 모사가 가능하다

: 3-MLP로 중간층에 있는 노드를 무한대로 쓰면 그 어떤 문제도 해결이 가능하다

 

 

5. Feedforward Process

- Input layer (입력층)

: layer는 보통 1개

: 값을 받아서 전달해주는 역할 (활성함수는 y=x가 됨)

: 노드의 개수는 변수의 개수 만큼

 

- Output Layer (출력층)

: layer 수는 보통 1개

: 노드 개수는 문제마다 정해져있음

 

- Hidden Layer (은닉층)

: 역할은 명확하지 않음

: layer의 개수는 표현 찾기 / 공간 왜곡 개수

: Node 개수는 복잡도 (ex. 2차원->5차원)

 

보통의 NN은 앞쪽으로 움직이는 구조 : Feedforward